7 SPIKNUTI
Zobrazit řešeníMinimalistické zadání se skládá z 36 cm dlouhé čáry, obrázků mnicha, kozy, zajíce a krávy a měřítka, které má ale jako jednotku stupně. Podle měřítka má tedy čára 360 stupňů, což je kruh.
Ve spojení s Horalkou, kterou jsme dostali, nás napadne, že obrázky představují čtyři brněnské hory – Mniší horu, Kozí horu, Zaječí horu a Kraví horu. Navíc umíme změřit jejich přesnou polohu na čáře (v přesném změření nám pomáhají drobné šedé čárky).
Nyní jsou dva způsoby, jak můžeme pokračovat.
První způsob: Čára nám připomíná horizont, na kterém vidíme hory. Obrázek tedy popisuje místo, ze kterého vidíme tyto čtyři hory tak, že mezi nimi jsou určité úhly. Takový bod lze konstrukčně získat pomocí ekvigonál (množin bodů, ze kterých je daná úsečka vidět pod daným úhlem), což je středoškolská geometrie, o které jste netušili, že by se vám někdy v životě mohla hodit. Postup se potvrzuje tím, že se všechny ekvigonály protnou v jednom bodě, požadovaný bod tedy existuje.
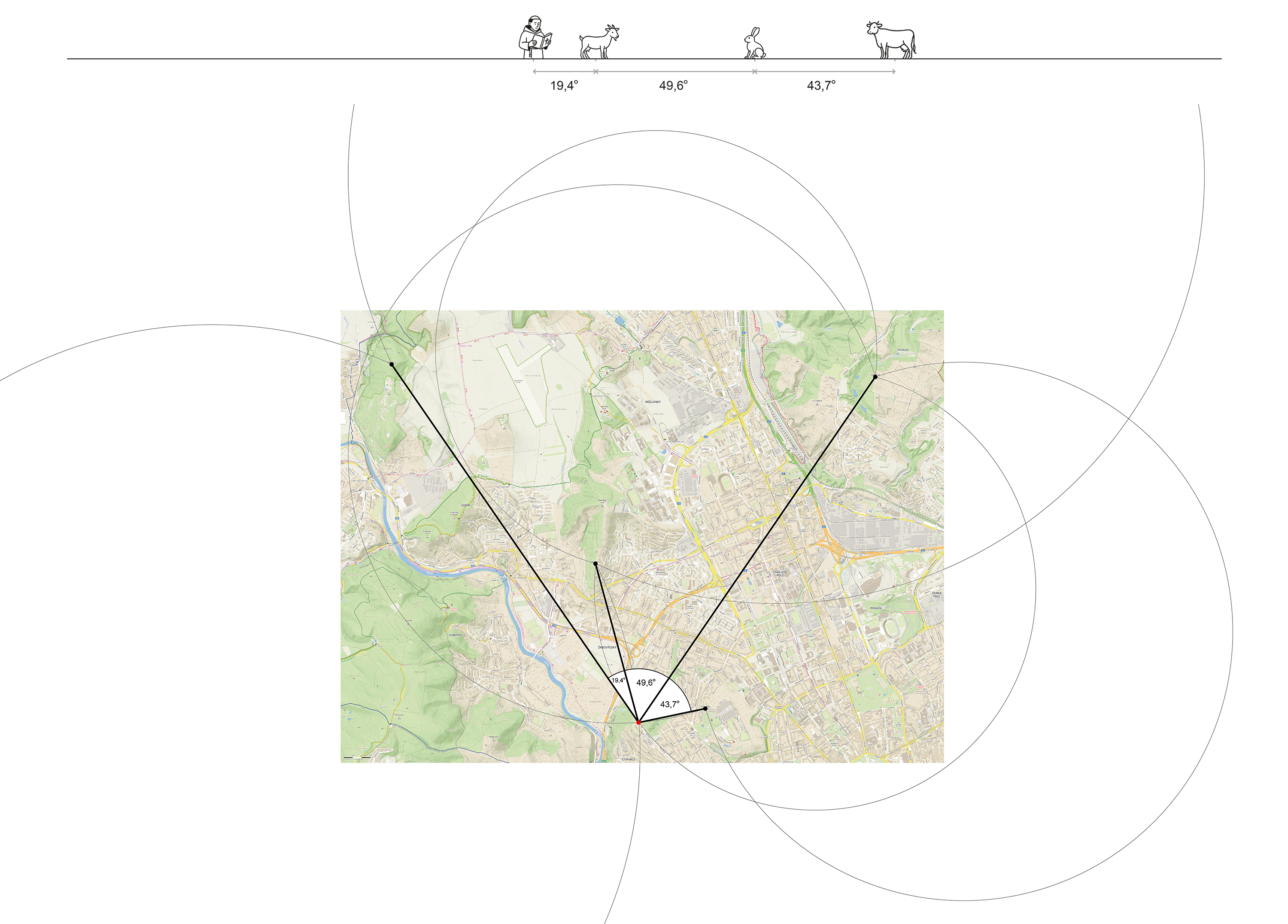
Druhý způsob: Vzdálenost hory od levého okraje čáry interpretujeme jako azimut. Když na mapě z každé hory narýsujeme polopřímku s jejím azimutem, všechny polopřímky se nám protnou v jednom bodě.
Bod, který jsme získali, je vyhlídka ve Wilsonově lese, což potvrzuje správnost postupu – vyhlídka je místo, ze kterého jdou vidět na obzoru hory. Dokonce když na této vyhlídce stojíte, díváte se přesně doprostřed čáry (severním směrem), nákres tedy odpovídá. Další stanoviště se nachází na vyhlídce nad bývalou sjezdovkou.